The original support vector machine (SVM), introduced in 1992 [2, 19, 43], can be characterized as a supervised learning algorithm capable of solving linear and non-linear classification problems. In comparison to neural networks we may describe SVM as a feed-forward neural net with one hidden layer (Fig. 6).
The main building blocks of SVM’s are structural risk minimisation, originating from statistical learning theory which was mainly developed by VAPNIK and CHERVONENKIS [17] , non-linear optimisation and duality and kernel induced features spaces [7, 8], underlining the technique with an exact mathematical framework.
Meanwhile, several extensions to the basic SVM have been introduced, e.g. for multi-class classification as well as regression and clustering problems, making the technique broadly applicable in the data mining area; see for example [47].

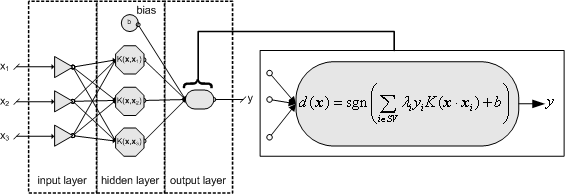
Fig. 6: Architecture of SVM classifier with linear or non-linear kernel function [6].

The main idea of support vector classification is to separate examples with a linear decision surface and maximize the margin between the different classes. This leads to the convex quadratic programming problem (the primal form was omitted for brevity, see for example [8]).

The Lagrange multiplier measures the influence of the i’th learning example on the functional W. Examples for which is positive are called support vectors, as they define the separating hyperplane. C is a constant cost parameter, controlling the number of support vectors and enabling the user to control the trade-off between learning error and model complexity, regarded by the margin of the separating hyperplane [41]. As complexity is considered directly during the learning stage, the risk of overfitting the training data is less severe for SVM. The separation rule is given by the indicator function using the dot product between the pattern to be classified (x), the support vectors and a constant threshold b.
For constructing more general non-linear decision functions, SVMs implement the idea to map the examples from input space X into a high-dimensional feature space  via an a priori chosen non-linear mapping function. The construction of a separating hyperplane in the features space leads to a non-linear decision surface in the original space; see Fig. 7. Expensive calculation of dot products in a high-dimensional space can be avoided by introducing a kernel function [5]. Leaving the algorithms almost unchanged, this reduces numerical complexity significantly and allows efficient support vector learning for up to hundreds of thousands examples. The modified decision function is given in Fig. 7.
Thus, the method is very flexible as a variety of learning machines can be constructed simply by using different kernel functions. The conditions a function has to fulfil in order to be applicable as a kernel (Mercer conditions) are described in [44]. Common kernels include polynomials of degree d and radial basis function classifiers with smoothing parameter.

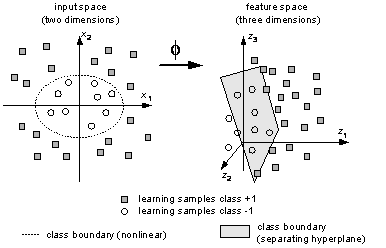
Fig. 7: Non-linear -mapping from two-dimensional input space with non-linear class boundaries into a three-dimensional feature space with linear separation by a hyperplane

Compared to neural networks the SVM method offers a significantly smaller number of parameters. The main modelling freedom consist in the choice of a kernel function and the corresponding kernel parameters, influencing the speed of convergence and the quality of results. Furthermore, the choice of the cost parameter C is vital to obtain good classification results, although algorithmic modifications can further simplify this task [16].

Home | Neural Associations | Neural Applications | Neural Data Sources | Neural Community | Neural Contacts | Neural Publications | Neural News&Events | Neural Software | Neural Tutorials | Neural Links | Forecasting Principles

©  2002-2005 BI³S-lab - Hamburg, Germany - All rights reserved - Questions, Comments and Enquiries via eMail -  [Impressum & Disclaimer]
The Knowledge Portal on Forecasting with Neural Networks @ www.neural-forecasting.com -