Please excuse the lack of content while we relaunch this part of the portal! We would appreciate your input ...

Artificial neural networks (ANN) offer great flexibility in modelling quantitative forecasting methods. Although error measures play an equally important role in explanatory forecasting, modelling causal relationships of variables or between multiple time series [22], this first analysis is limited to time-series point predictions with neural networks. Therefore, a variable is predicted using only observations of the same variable , interpreting the time t as the only independent variable.[16]
Following, we consider a feed-forward multilayer perceptron (MLP) of an arbitrary topology; for the impact of alternative network architectures on time series prediction see Azoff [5] or Zimmerer [26]. At a point in time t (t=1,…,T), a one-step ahead forecast is computed using observations from n preceding points in time t, t-1, t-2, …, t-n-1, with n (n=1,…,N) denoting the number of input units. This models a time-series prediction in analogy to an non-linear autoregressive AR(n) model [16] of the form (1)

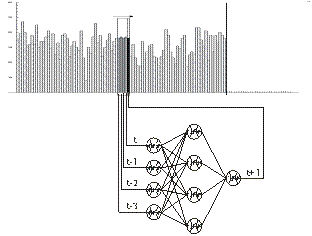A network architecture is displayed in figure 1, showing Neural Network application to time series forecasting with a (4-4-1) MLP, using n=4 input neurons for observations in t, t-1, t-2, t-3, four hidden units, one output neuron for time period t+1 and two layers of 20 trainable weights. [23].

The task of the MLP is to model the underlying generator of the data during training, so that a valid forecast is made when the trained network is subsequently presented with a new value for the input vector. [6]
Unless a network is perfectly trained, these network outputs differ from the desired outputs. The network learns the underlying relationship through minimization of this difference on the training data. The real-world significance of these deviations depends on the application and is measured by an objective function, also called error function, whose output rates the quality of the networks response. [18] As the specification and estimation of an objective function calls for an actual application, we consider alternative error functions for sales predictions in inventory management.
In forecasting with ANNs, as in prediction in general, error functions are applied in all phases of modelling, network selection and application. During modelling, errors measures are computed and minimised to estimate parameters fitting a forecasting method to the data, in neural network terminology referred to as training. After finding valid parameters, error measures are calculated to verify the ex post quality of a single method, to compare forecast results of different architectures of a method or to compare results of competing methods. During the application of a chosen method, error measures may act as tracking-signals for constant evaluation, model-adaptation or retraining. [20] Although error functions play a predominant role in neural network forecasting, standard statistical error measures are routinely used instead of the actual objective function. As the training of a network determines its validity and reliability in forecasting, we focus the following analysis on the use of error measures as objective functions for ANN training.

©  

©  2002-2005 BI³S-lab - Hamburg, Germany - All rights reserved - Questions, Comments and Enquiries via eMail -  [Impressum & Disclaimer]
The Knowledge Portal on Forecasting with Neural Networks @ www.neural-forecasting.com -